高二年级数学上册（第1.1.1-1课时）《正弦定理》PPT教学课件

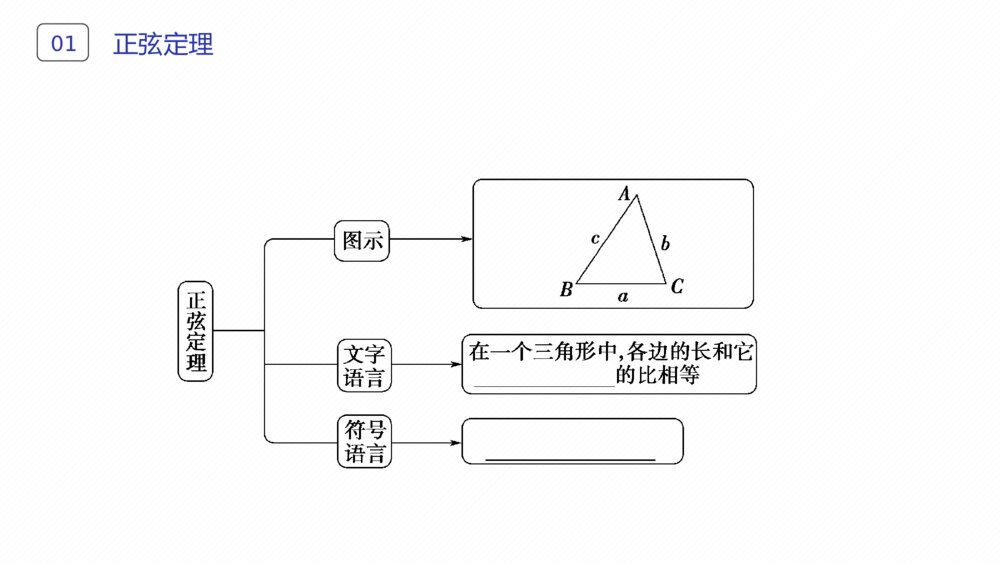
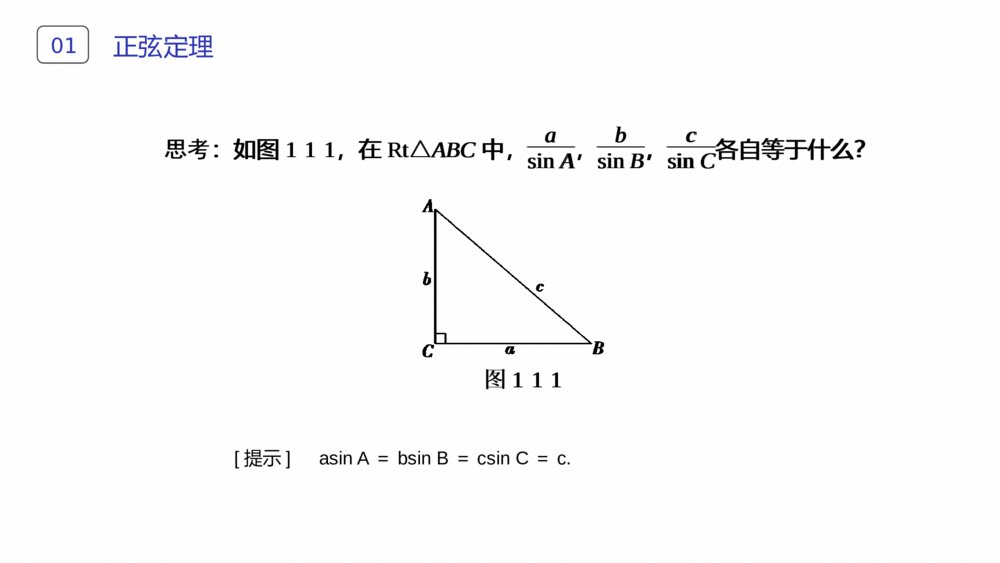
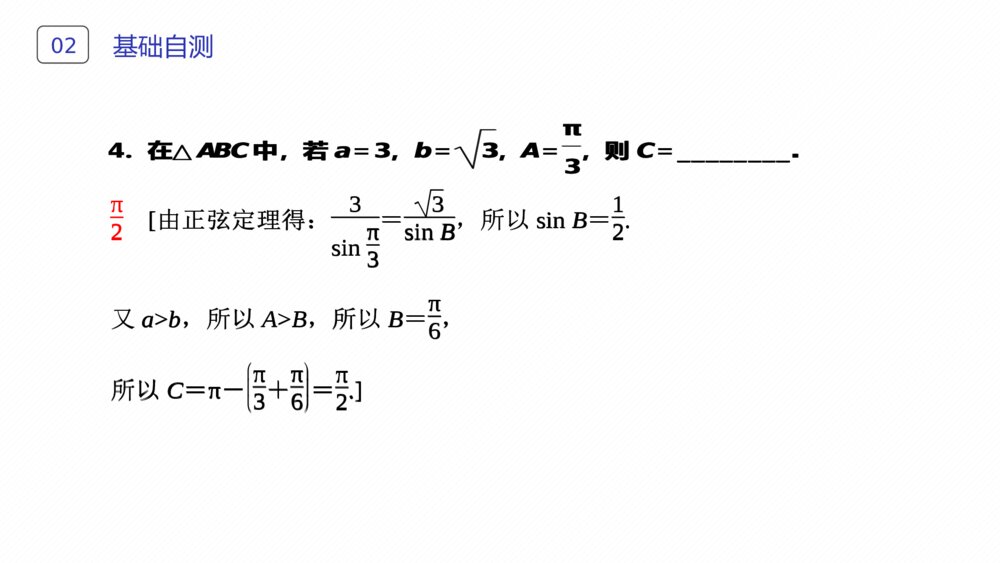
主讲人：XXX第一章解三角形1.1.1正弦定理（第1课时）正弦定理和余弦定理目录CONTENS学习目标LEARNINGOBJECTIVES011.通过对任意三角形边长和角度关系的探索，掌握正弦定理的内容及其证明(难点).2.能运用正弦定理与三角形内角和定理解决简单的解三角形问题(重点)．01学习目标LEARNINGOBJECTIVES正弦定理01正弦定理01[提示]　asinA＝bsinB＝csinC＝c.思考：如图1­1­1，在Rt△ABC中，asin­A，bsin­B，csin­C各自等于什么？­­图1­1­1­思考：如图1­1­1，在Rt△ABC中，asin­A，bsin­B，csin­C各自等于什么？­­图1­1­1­解三角形02[提示]　利用正弦定理可以解决以下两类有关三角形的问题：①已知两角和任意一边，求其他两边和第三个角；②已知两边和其中一边的对角，求另一边的对角，从而求出其他的边和角．(1)一般地，把三角形的和它们的叫做三角形的元素．(2)已知三角形的几个元素求的过程叫做解三角形．思考：利用正弦定理可以解决哪两类有关三角形问题？三个角A，B，C对边a，b，c其他元素基础自测021．思考辨析(1)正弦定理只适用于锐角三角形．(　　)(2)正弦定理不适用于直角三角形．(　　)(3)在某一确定的三角形中，各边与它所对的角的正弦的比值是一定值．(　　)[答案]　(1)×　(2)×　(3)√提示：正弦定理适用于任意三角形，故(1)(2)均不正确．基础自测022．在△ABC中，若A＝60°，B＝45°，BC＝32，则AC＝________.23　[由正弦定理得：32sin60°＝ACsin45°，所以AC＝32×sin45°sin60°＝23.]3．在△ABC中，A＝45°，c＝2，则AC边上的高等于______________．2　[AC边上的高为ABsinA＝csinA＝2sin45°＝2.]2．在△ABC中，若A＝60°，B＝45°，BC＝32，则AC＝________.23[由正弦定理得：32sin60°＝ACsin45°，所以AC＝32×sin45°sin60°＝23.]3．在△ABC中，A＝45°，c＝2，则AC边上的高等于______________．2[AC边上的高为ABsinA＝csinA＝2sin45°＝2.]基础自测022．在△ABC中，若A＝60°，B＝45°，BC＝32，则AC＝________.23[由正弦定理得：32sin60°＝ACsin45°，所以AC＝32×sin45°sin60°＝23.]3．在△ABC中，A＝45°，c＝2，则AC边上的高等于______________．2[AC边上的高为ABsinA＝csinA＝2sin45°＝2.]4．在△ABC中，若a＝3，b＝3，A＝π3，则C＝________.π2[由正弦定理得：3sin­π3＝3sin­B，所以sin­B＝12.­又a>b，所以A>B，所以B＝π6，­所以C＝π－π3＋π6＝π2.]­基础自测024．在△ABC中，若a＝3，b＝3，A＝π3，则C＝________.π2[由正弦定理得：3sin­π3＝3sin­B，所以sin­B＝12.­又a>b，所以A>B，所以B＝π6，­所以C＝π－π3＋π6＝π2.]­[合作探究·攻重难]定理证明例1、在钝角△ABC中，证明正弦定理．[证明]如图，过C作CD⊥AB，垂足为D，D是BA延长线上一点，根据正弦函数的定义知：基础自测02[合作探究·攻重难]定理证明例1、在钝角△ABC中，证明正弦定理．[证明]如图，过C作CD⊥AB，垂足为D，D是BA延长线上一点，根据正弦函数的定义知：基础自测02CDb＝sin∠CAD＝sin(180°－A)＝sinA，CDa＝sinB.∴CD＝bsinA＝asinB.∴asinA＝bsinB.同理，bsinB＝csinC.故asinA＝bsinB＝csinC.CDb＝sin∠CAD＝sin(180°－A)＝sinA，CDa＝sinB.∴CD＝bsinA＝asinB.∴asinA＝bsinB.同理，bsinB＝csinC.故asinA＝bsinB＝csinC.基础自测02[规律方法](1)本例用正弦函数定义沟通边与角内在联,系，充分挖掘这些联系可以使你理解更深刻，记忆更牢固.(2)要证asinA＝bsinB，只需证asinB＝bsinA，而asinB，bsinA都对应CD.初看是神来之笔，仔细体会还是有迹可循的，通过体会思维的轨迹，可以提高我们的分析解题能力.[规律方法](1)本例用正弦函数定义沟通边与角内在联,系，充分挖掘这些联系可以使你理解更深刻，记忆更牢固.(2)要证asinA＝bsinB，只需证asinB＝bsinA，而asinB，bsinA都对应CD.初看是神来之笔，仔细体会还是有迹可循的，通过体会思维的轨迹，可以提高我们的分析解题能力.跟踪训练021．如图112，锐角△ABC的外接圆O半径为R，证明asinA＝2R.图1121．如图112，锐角△ABC的外接圆O半径为R，证明asinA＝2R.图112跟踪训练02[证明]连接BO并延长，交外接圆于点A′，连接A′C，则圆周角∠A′＝∠A.∵A′B为直径，长度为2R，∴∠A′CB＝90°，∴sinA′＝BCA′B＝a2R，∴sinA＝a2R，即asinA＝2R.[证明]连接BO并延长，交外接圆于点A′，连接A′C，则圆周角∠A′＝∠A.∵A′B为直径，长度为2R，∴∠A′CB＝90°，∴sinA′＝BCA′B＝a2R，∴sinA＝a2R，即asinA＝2R.跟踪训练02用正弦定理解三角形例2、已知△ABC中，a＝10，A＝30°，C＝45°，求角B，边b，c.思路探究：①角A，B，C满足什么关系？②105°可拆分成哪两个特殊角的和？③由正弦定理如何求得b，c的值？用正弦定理解三角形例2、已知△ABC中，a＝10，A＝30°，C＝45°，求角B，边b，c.思路探究：①角A，B，C满足什么关系？②105°可拆分成哪两个特殊角的和？③由正弦定理如何求得b，c的值？跟踪训练02[解]∵A＝30°，C＝45°，∴B＝180°－(A＋C)＝105°，又由正弦定理得：c＝asinCsinA＝102.b＝asinBsinA＝10·sin105°sin30°＝20sin(60°＋45°)＝5(6＋2)．∴B＝105°，b＝5(6＋2)，c＝102.[解]∵A＝30°，C＝45°，∴B＝180°－(A＋C)＝105°，又由正弦定理得：c＝asinCsinA＝102.b＝asinBsinA＝10·sin105°sin30°＝20sin(60°＋45°)＝5(6＋2)．∴B＝105°，b＝5(6＋2)，c＝102.规律方法02(1)正弦定理实际上是三个等式：asinA＝bsinB，bsinB＝csinC，asinA＝csinC，每个等式涉及四个元素，所以只要知道其中的三个就可以求另外一个.(2)具体地说，以下两种情形适用正弦定理：①已知三角形的任意两角与一边；②已知三角形的任意两边与其中一边的对角.(1)正弦定理实际上是三个等式：asinA＝bsinB，bsinB＝csinC，asinA＝csinC，每个等式涉及四个元素，所以只要知道其中的三个就可以求另外一个.(2)具体地说，以下两种情形适用正弦定理：①已知三角形的任意两角与一边；②已知三角形的任意两边与其中一边的对角.跟踪训练022．已知∠B＝30°，b＝2，c＝2，求A、C、a.[解]由正弦定理得：sinC＝c·sinBb＝2sin30°2＝22，∵c>b,0°b,0°b，∴A>B＝45°.∴A＝60°或120°.当A＝60°时，C＝180°－45°－60°＝75°，c＝bsinCsinB＝2sin75°sin45°＝6＋22；【答案】5．已知在△ABC中，a＝3，b＝2，B＝45°，解这个三角形．由正弦定理及已知条件有3sinA＝2sin45°，得sinA＝32.∵a>b，∴A>B＝45°.∴A＝60°或120°.当A＝60°时，C＝180°－45°－60°＝75°，c＝bsinCsinB＝2sin75°sin45°＝6＋22；练一练02当A＝120°时，C＝180°－45°－120°＝15°，c＝bsinCsinB＝2sin15°sin45°＝6－22.综上，可知A＝60°，C＝75°，c＝6＋22或A＝120°，C＝15°，c＝6－22.当A＝120°时，C＝180°－45°－120°＝15°，c＝bsinCsinB＝2sin15°sin45°＝6－22.综上，可知A＝60°，C＝75°，c＝6＋22或A＝120°，C＝15°，c＝6－22.主讲人：XXX第一章解三角形THANKYOUFORLISTENING谢谢各位同学倾听