







《2012新课标文科数学回归教材《4三角函数》》是由用户上传到老师板报网,本为文库资料,大小为565 KB,总共有9页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 9页
- 565 KB
- VIP模板
- doc
- 数字产品不支持退货
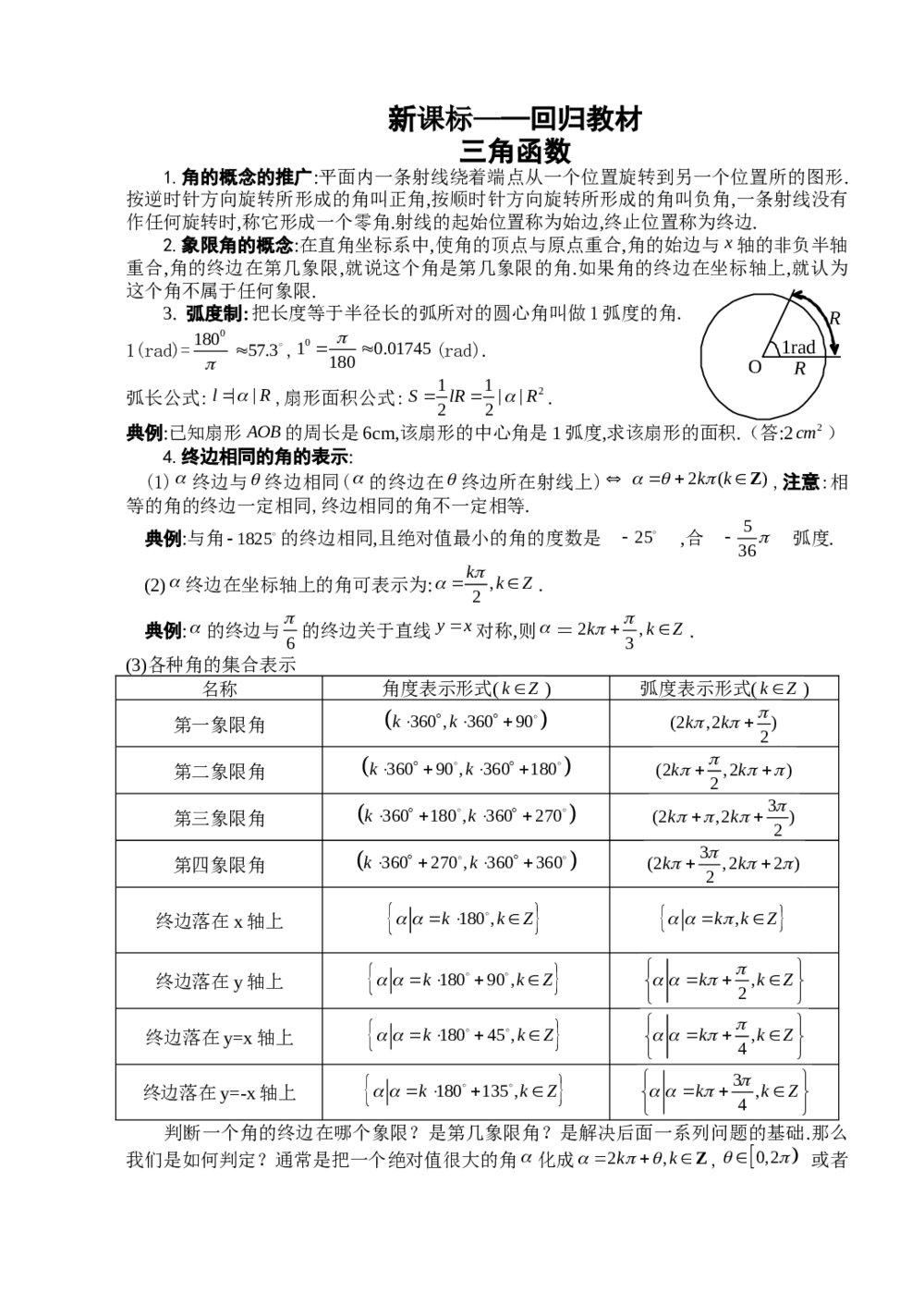
OR1radR新课标——回归教材三角函数1.角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形.按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角.射线的起始位置称为始边,终止位置称为终边.2.象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角.如果角的终边在坐标轴上,就认为这个角不属于任何象限.3.弧度制:把长度等于半径长的弧所对的圆心角叫做1弧度的角.1(rad)=018057.3,010.01745180(rad).弧长公式:||lR,扇形面积公式:211||22SlRR.典例:已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积.(答:22cm)4.终边相同的角的表示:(1)终边与终边相同(的终边在终边所在射线上)2()kkZ,注意:相等的角的终边一定相同,终边相同的角不一定相等.典例:与角1825的终边相同,且绝对值最小的角的度数是25,合536弧度.(2)终边在坐标轴上的角可表示为:,2kkZ.典例:的终边与6的终边关于直线yx对称,则=2,3kkZ.(3)各种角的集合表示名称角度表示形式(kZ)弧度表示形式(kZ)第一象限角360,36090kk(2,2)2kk第二象限角36090,360180kk(2,2)2kk第三象限角360180,360270kk3(2,2)2kk第四象限角360270,360360kk3(2,22)2kk终边落在x轴上180,kkZ,kkZ终边落在y轴上18090,kkZ,2kkZ终边落在y=x轴上18045,kkZ,4kkZ终边落在y=-x轴上180135,kkZ3,4kkZ判断一个角的终边在哪个象限?是第几象限角?是解决后面一系列问题的基础.那么我们是如何判定?通常是把一个绝对值很大的角化成2,kkZ,0,2或者xyTAMPO是化成360,,0,360kkZ,这样只要判定是第几象限角就可以了.典例:(1)291033,因为3是第一象限角,所以293的终边也在第一象限;(2)790236070,因为70是第一象限角,所以790的终边也在第一象限.5.与2的终边关系:由“两等分各象限、一二三四”确定.如图,若角终边在第一(二、三、四)象限,则角2的终边位于右图中标有数字1(2、3、4)区域.这个方法叫做等分象限法.典例:若是第二象限角,则2是第一、三象限角.6.任意角的三角函数的定义:设是任意一个角,P(,)xy是的终边上的任意一点(异于原点),它与原点的距离是220rxy,那么sin,cosyxrr,tan0yxx.三角函数值只与角的大小有关,而与终边上点P的位置无关.典例:(1)已知角的终边经过点P(5,-12),则sincos的值为713;(2)设是第三、四象限角,23sin4mm,则m的取值范围是32(1,);(3)若|sin|cos0sin|cos|,试判断cot(sin)tan(cos)的符号(答:负)7.三角函数线的特征是:正弦线MP“站在x轴上(起点在x轴上)”、余弦线OM“躺在x轴上(起点是原点)”、正切线AT“与圆O切在点(1,0)A处(起点是A)”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式.典例:(1)若08,则sin,cos,tan的大小关系为tansincos;(2)若为锐角,则,sin,tan的大小关系为sintan;(3)函数12coslg(2sin3)yxx的定义域是2(2,2]()33kkkZ8.特殊角的三角函数值:30°45°60°0°90°180°270°15°75°sin122232010-1624624cos32221210-10624624tan3313002-32+3cot3133002+32-39.同角三角函数的基本关系式:(1)平方关系:22sincos1;(2)商数关系:sintancos.yx12341234y=xy=-x同角三角函数的基本关系式的主要应用是,已知一个角的三角函数值,求此角的其它三角函数值.在运用平方关系解题时,要根据已知角的范围和三角函数的取值,尽可能地压缩角的范围,以便进行定号;在具体求三角函数值时,一般不需用同角三角函数的基本关系式,而是先根据角的范围确定三角函数值的符号,再利用解直角三角形求出此三角函数值的绝对值.解题方法总结(1)已知一弦值,求正切.通常是利用2sin1cos、2cos1sin求另一弦值,然后利用sintancos求正切.要注意的象限,分象限定符号.(2)已知正切,求正弦、余弦值.方法一是解方程组.方法二是利用一个推导公式直接求,公式221cos1tan,222tansin1tan,不过还是要注意开根号时的正负的确定.(3)解题中常用的三种技巧:一、切化弦;二、1的代换;三、分子分母同时除以cos或者2cos.(4)解题中常用的两组公式:222(sincos)sincos2sincos12sincos;222(sincos)sincos2sincos12sincos.典例:(1)函数sintancoscoty的值的符号为大于0;(2)若022x,则使21sin2cos2xx成立的x的取值范围是3[0,][,]44;(3)已知3sin5mm,42cos()52mm,则tan=512;(4)已知tan1tan1,则sin3cossincos=53;2sinsincos2=135;(5)已知sin200a,则tan160等于BA.21aa B.21aa C.21aa D.21aa;(6)已知(cos)cos3fxx,则(sin30)f的值为-1.10.三角函数诱导公式(2k)的本质是:奇变偶不变(对k而言,指k取奇数或偶数),符号看象限(看原函数,同时可把看成是锐角).诱导公式的应用是求任意角的三角函数值,其一般步骤:“负化正,大化小,化成锐角再查表”即:(1)负角变正角,再写成2k+,02;(2)转化为锐角三角函数.典例:(1)97costan()sin2146的值为2323;(2)已知4sin(540)5,则cos(270)45,若为第二象限角,则2[sin(180)cos(360)]tan(180)3100.11.两角和与差的正弦、余弦、正切公式及倍角公式:正:sinsincoscossin;逆:22sincossin()abab,其中tanba.正:coscoscossinsin;逆:22cossincos()abab,其中tanba.正:tantantan1tantan;变:tantantan()(1tantan).正:22tansin22sincos1tan;变:21sin2(sincos)正:2222221tancos22cos112sincossin1tan;变:221cos22cos,1cos22sin(降角升幂公式),逆:221+cos21cos2cos,sin22==(降幂升角公式);sin1costan21cossin(半角正切)典例:(1)下列各式中,值为12的是CA.sin15cos15B.22cossin1212 C.2tan22.51tan22.5D.1cos302(2)命题P:tan()0AB,命题Q:tantan0AB,则P是Q的C条件.A、充要 B、充分不必要 C、必要不充分 D、既不充分也不必要;(3)已知3sin()coscos()sin5,那么cos2的值为725;(4)13sin10sin80的值是4;(5)已知0tan110a,求0tan50的值(用a表示)甲求得的结果是313aa,乙求得的结果是212aa,对甲、乙求得的结果的正确性你的判断是甲、乙都对.12.三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构.即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点通常是分式要因式分解、通分后约分、根号下配方后开方.基本的技巧有:★★★(1)巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换.如:()(),2()(),2()(),22,222等.典例:(1)已知2tan()5,1tan()44,那么tan()4的值是322;(2)已知02,且1cos()29,2sin()23,求cos()的值239729;(3)若,为锐角,3sin,cos,cos()5xy,则y与x的函数关系为23431(1)555yxxx.(2)三角函数名互化(切化弦),典例:(1)求值sin50(13tan10)=1;(2)已知sincos21,tan()1cos23,求tan(2)的值18(3)公式变形使用(tantantan1tantan.典例:(1)已知A、B为锐角,且满足tantantantan1ABAB,则cos()AB=22;(2)ABC中,tantan33tantanABAB,3sincos4AA,则此三角形是等边三角形.(4)三角函数次数的降升(降幂公式:21cos2cos2,21cos2sin2与升幂公式:21cos22cos,21cos22sin).典例:(1)若3(,)2,化简1111cos22222为sin2;(2)2()5sincos53cosfxxxx53()2xR的单调递增区间为5[,]()1212kkkZ.(5)式子结构的转化(对角、函数名、式子结构化同).典例:(1)tan(cossin)sintancotcsc=sin;(2)求证:21tan1sin212sin1tan22;(3)化简:42212cos2cos22tan()sin()44xxxx=1cos22x.(6)常值变换主要指“1”的变换(221sincosxxtansin42等)典例:已知tan2,求22sinsincos3cos=35.(7)正余弦“三兄妹—sincossincosxxxx、”的内存联系—“知一求二”.典例:(1)若sincosxxt,则sincosxx212t,特别提醒:这里[2,2]t;(2)若1(0,),sincos2,求tan的值.(答:473);(3)已知2sin22sin1tank()42,试用k表示sincos的值(答:1k).13.辅助角公式中辅助角的确定:22sincossinaxbxabx(其中角所在的象限由a,b的符号确定,角的值由tanba确定)在求最值、化简时起作用.★★★典例:(1)若方程sin3cosxxc有实数解,则c的取值范围是[-2,2].;(2)当函数2cos3sinyxx取得最大值时,tanx的值是32;(3)如果sin2cos()fxxx是奇函数,则tan=-2;(4)求值:2223164sin20sin20cos2032.14.正弦函数和余弦函数的图象:正弦函数sinyx和余弦函数cosyx图象的作图方法:五点法:先取横坐标分别为0,,23,,22的五点,再用光滑的曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象.如右图所示:15.正弦函数sin()yxxR、余弦函数cos()yxxR性质:(1)定义域R.(2)值域1,1.对sinyx,当22xkkZ时,y取最大值1;当322xkkZ时,y取最小值-1;对cosyx,当2xkkZ时,y取最大值1,当2xkkZ时,y取最小值-1.典例:(1)若函数sin(3)6yabx的最大值为32,最小值为12,则a12,b1;(2)函数()sin3cosfxxx([,]22x)的值域是[-1,2];(3)若2,则cos6siny的最大值和最小值分别是7、-5;(4)2()2cossin()3sin3fxxxxsincosxx的最小值是2,此时x=()12kkZ;(5)己知1sincos2,则sincost的取值范围11[,]22;(6)若22sin2sin2cos,则22sinsiny的最大值1、最小值222.特别提醒:在解含有正余弦函数的问题时,你深入挖掘正余弦函数的有界性了吗?例如前面的关于求值域的一个运用!(3)周期性:①sinyx、cosyx的最小正周期都是2;②()sin()fxAx和()cos()fxAx的最小正周期都是2||T.典例:(1)若()sin3xfx,则(1)(2)(3)(2003)ffff=0;(2)函数4()cosfxx2sincosxx4sinx的最小正周期为;(3)设()2sin()25fxx,若12()()()()fxfxfxxR恒成立,则12min||xx=2.(4)奇偶性与对称性:①函数sin()yxxR是奇函数,对称中心是,0kkZ,对称轴是直线2xkkZ;②函数cos()yxxR是偶函数,对称中心是,02kkZ,对称轴是直线xkkZ(正(余)弦型函数的对称轴为过最值点且垂直于x轴的直线,对称中心为图象零点所在点.)典例:(1)函数5sin22yx的奇偶性是偶函数;(2)已知函数3()sin1(,fxaxbxab为常数),且(5)7f,则(5)f-5;(3)2cos(sincos)yxxx的对称中心和对称轴分别是(,1)()28kkZ、()28kxkZ;(4)已知()sin()3cos()fxxx为偶函数,求的值.(答:()6kkZ)(5)单调性:sin2,222yxkkkZ在上单调递增,在32,222kkkZ单调递减;cosyx在2,2kkkZ上单调递减,在2,22kkkZ上单调递增.16.形如sin()yAx的函数:(1)几个物理量:A―振幅;1fT―频率(周期的倒数);x―相位;―初相;(2)求sin()yAx表达式:A由最值确定;由周期确定;由图象上的特殊点确定.(3)函数sin()yAx图象的画法:①“五点法”—设Xx,令X=0,3,,,222求出相应的x值,计算得出五点的坐标,描点后得出图象;②图象变换法:这是作函数简图常用方法.(4)函数sin()yAxk的图象与sinyx图象间的关系:①sinyx的图象上各点向左(>0)或向右(<0)平移||个单位得sinyx的图象;②sinyx图象的纵坐标不变,横坐标变为原来的1,得到函数sinyx的图象;③sinyx图象上各点横坐标不变,纵坐标变为原来的A倍,得sin()yAx图象;④sin()yAx图象上各点向上(0k)或向下(0k),得到sinyAxk的图象.特别注意:由sinyx得到sinyx的图象,则向左或向右平移应平移||单位.典例:(1)函数2sin(2)14yx的图象经过怎样的变换才能得到sinyx的图象?(答:2sin(2)14yx向上平移1个单位得2sin(2)4yx的图象,再向左平移8个单位得2sin2yx的图象,横坐标扩大到原来的2倍得2sinyx的图象,最后将纵坐标缩小到原来的12即得sinyx的图象);(2)要得到函数cos()24xy的图象,只需把函数sin2xy的图象向左平移2个单位;(3)(现在考纲不作要求)将函数72sin(2)13yx图像,按向量a平移后得到的函数图像关于原点对称,这样的向量是否唯一?若唯一,求出a;若不唯一,求出模最小的向量(答:存在但不唯一,模最小的向量(,1)6a);(4)若函数cossin0,2fxxxx的图象与直线yk有且仅有四个不同的交点,则k的取值范围是[1,2).(5)研究函数sin()yAx性质的方法:类比于研究sinyx的性质,只需将sin()yAx中的x看成sinyx中的x,但在求sin()yAx的单调区间时,要特别注意A和的符号,通过诱导公式先将化正.典例:(1)函数sin(2)3yx的递减区间是5[,]()1212kkkZ;(2)12logcos()34xy的递减区间是33[6,6]()44kkkZ;(3)设函数()sin()(0,0,)22fxAxA的图象关于直线23x对称,它的周期是,则(C)A、1()(0,)2fx的图象过点 B、()fx在区间52[,]123上是减函数 C、5()(,0)12fx的图象的一个对称中心是 D、()fx的最大值是A;(4)对于函数2sin23fxx给出下列结论,其中正确结论是②④.①图象关于原点成中心对称;②图象关于直线12x成轴对称;③图象可由函数2sin2yx的图像向左平移3个单位得到;④图像向左平移12个单位,即得到函数2cos2yx的图像.(5)已知函数()2sin()fxx图象与直线1y的交点中,距离最近两点间的距离为3,那么此函数的周期是17.正切函数tanyx的图象和性质:(1)定义域:{|,}2xxkkZ.有关正切函数问题时,你注意到正切函数的定义域了吗?(2)值域是R,在上面定义域上无最大值也无最小值;(3)周期性:,它与直线ya的两个相邻交点之间的距离是一个周期.绝对值或平方对三角函数周期性的影响:一般说来,某一周期函数解析式加绝对值或平方,其周期性是:弦减半、切不变.既为周期函数又是偶函数的函数自变量加绝对值,其周期性不变,其它不定.(只作了解即可)典例:(1)2sin,sinyxyx,|tan|yx的周期都是.(2)sinyxcosx的周期为2.(3)1|2sin(3)|,|2sin(3)2|626yxyx的周期都是2;(4)tanyx奇偶性与对称性:是奇函数,对称中心是,02kkZ.特别提醒:正切型函数的对称中心有两类:一类是图象与x轴的交点,另一类是渐近线与x轴的交点,但无对称轴,这是与正弦、余弦函数的不同之处.(5)单调性:正切函数在开区间(,)22kkkZ内都是增函数.但要注意在整个定义域上不具有单调性.18.三角形中的有关公式:(1)内角和定理:三角形三角和为,这是三角形中三角函数问题的特殊性,解题可不能忘记!任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.锐角三角形三内角都是锐角三内角的余弦值为正值任两角和都是钝角任意两边的平方和大于第三边的平方.(2)正弦定理:2sinsinsinabcRABC(R为三角形外接圆的半径).注意:①正弦定理的一些变式:sinsinsiniabcABC;sin,sin,sin22abiiABCRR2cR;2sin,2sin,2siniiiaRAbRBbRC;②已知三角形两边一对角,求解三角形时,若运用正弦定理,则务必注意可能有两解.(3)余弦定理:2222222cos,cos2bcaabcbcAAbc等,常选用余弦定理鉴定三角形形状.(4)面积公式:111sin()222aSahabCrabc(其中r为三角形内切圆半径).海伦-秦九韶公式()()()Sppapbpc,其中2abcp.典例:ABC中,若22222sincoscossinsinABABC,判断ABC的形状(答:直角三角形).特别提醒:(1)求解三角形中的问题时,一定要注意ABC这个特殊性:所以有,,sin()sin,sincos22ABCABCABC;(2)求解三角形中含有边角混合关系的问题时,常运用正弦定理、余弦定理实现边角互化.典例:(1)ABC中,A、B的对边分别是ab、,且A=60,6,4ab,那么满足条件的ABCA、有一个解B、有两个解C、无解D、不能确定(答:C);(2)在ABC中,A>B是sinsinAB成立的充要条件;(3)在ABC中,(1tan)(1tan)2AB,则2logsinC=12;(4)在ABC中,若()(sinsinabcABsin)3sinCaB,则C=60;(5)在ABC中,若其面积22243abcS,则C=30;(6)在ABC中,60,1Ab,这个三角形的面积为3,则ABC外接圆的直径是2393;(7)在△ABC中,213,cos,cos32BCaA则=13,22bc的最大值为92;(8)在△ABC中AB=1,BC=2,则角C的取值范围是06C;(9)设O是锐角三角形ABC的外心,若75C,且,,AOBBOCCOA的面积满足关系式3AOBBOCCOASSS,求A(答:45).19.求角的方法:先确定角的范围,再求出关于此角的某一个三角函数(要注意选择,其标准有二:一是此三角函数在角的范围内具有单调性;二是根据条件易求出此三角函数值).特别提示:要尽量利用已知条件精确地确定角所在的范围.典例:(1)若,(0,),且tan、tan是方程2560xx的两根,则求的值34;(2)ABC中,3sin4cos6,4sin3cos1ABBA,则C=3;(3)若02且sinsinsin0,coscoscos0,求的值(答:23).

















