









试读已结束,还剩19页未读,您可下载完整版后进行离线阅读
《2012届高考数学(理科)考前60天冲刺《数列专练》》是由用户上传到老师板报网,本为文库资料,大小为1.15 MB,总共有29页,格式为doc。授权方式为VIP用户下载,成为老师板报网VIP用户马上下载此课件。文件完整,下载后可编辑修改。
- 文库资料
- 29页
- 1.15 MB
- VIP模板
- doc
- 数字产品不支持退货
2012届高考数学(理)考前60天冲刺【六大解答题】数列专练1.数列}{na的前n项和记为nS,ta1,121()nnaSnN.(1)当t为何值时,数列}{na是等比数列;(2)在(I)的条件下,若等差数列}{nb的前n项和nT有最大值,且153T,又11ba,22ba,33ba成等比数列,求nT.2.已知数列na的首项114a的等比数列,其前n项和nS中3316S,(Ⅰ)求数列na的通项公式;(Ⅱ)设12log||nnba,12231111nnnTbbbbbb,求nT3.已知数列{}na的首项11a,且满足*1().41nnnaanNa(1)设1nnba,求证:数列{}nb是等差数列,并求数列{}na的通项公式;(2)设2nnncb,求数列{}nc的前n项和.nS4.已知}{na是单调递增的等差数列,首项31a,前n项和为nS,数列}{nb是等比数列,首项.20,12,123221bSbab且(Ⅰ)求}{}{nnba和的通项公式。(Ⅱ)令}{),)(cos(nnnncNnaSC求的前n项和.nT5.已知数列{}na的前n项和为nS,若112,.nnnnnnaSanbaa且(1)求证:{1}na为等比数列;(2)求数列{}nb的前n项和。6.在数列na中,已知)(121,1*111Nnaaaaaannnnn且(I)求数列na的通项公式;(II)令132212111,)12(nnnnnccccccSac,若kSn恒成立,求k的取值范围。8.已知数列na中,14a,12(1)nnaan,(1)求证:数列2nan为等比数列。(2)设数列na的前n项和为nS,若22nnSan,求正整数列n的最小值。9.已知数列{}na的前项和nS满足:(1)1nnaSaa(a为常数,且0a,1a).(Ⅰ)求{}na的通项公式;(Ⅱ)设21nnnSba,若数列{}nb为等比数列,求a的值.10.已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列.(1)求数列{an}的通项公式;(2)设Tn为数列{}的前n项和,若Tn≤λan+1对∀n∈N*恒成立,求实数λ的最小值.11.在各项均为正数的数列na中,已知点*1,()nnaanN在函数2yx的图像上,且24164aa.(Ⅰ)求证:数列na是等比数列,并求出其通项;(Ⅱ)若数列nb的前n项和为nS,且nnbna,求nS.12.数列na中,已知)(121,1*111Nnaaaaaannnnn且(I)求数列na的通项公式;(II)令132212111,)12(nnnnnccccccSac,若kSn恒成立,求k的取值范围。13.已知数列{}na的前n项和为nS,若112,.nnnnnnaSanbaa且(1)求证:{1}na为等比数列;(2)求数列{}nb的前n项和。14.在数列{}na中,13a,122nnaan(2n≥且*)nN.(1)求2a,3a的值;(2)证明:数列{}nan是等比数列,并求{}na的通项公式;(3)求数列{}na的前n项和nS.15.已知数列na满足222121naaann(Ⅰ)求数列na的通项;(Ⅱ)若nnanb求数列nb的前n项nS和。16.已知正项数列}{na的前n项和为nS,且*,21NnSaannn.(Ⅰ)求证:数列}{2nS是等差数列;(Ⅱ)求解关于n的不等式84)(11nSSannn、;(Ⅲ)记数列32nnSb,nnbbbT11121,证明:nTnn123111.17,已知递增的等比数列{}na满足234328,2aaaa且是24,aa的等差中项。(Ⅰ)求数列{}na的通项公式;(Ⅱ)若nnnSab,12log是数列{}nnab的前n项和,求.nS19.设na是公差不为零的等差数列,nS为其前n项和,满足222223457,7aaaaS,(1)求数列na的通项公式及前n项和nS;(2)试求所有的正整数m,使得12mmmaaa为数列na中的项。20.已知等差数列na满足:37a,5726aa,na的前n项和为nS.(Ⅰ)求na及nS;(Ⅱ)令bn=211na(*nN),求数列nb的前n项和nT。20.已知数列{an}的前n项和为Sn,且a1=1,nan+1=(n+2)Sn(n=1,2,3,…).(1)求证:数列{}为等比数列,并由此求出Sn;(2)若数列{bn}满足:b1=,=(n∈N*),试求数列{bn}的通项公式.21.已知数列{}na的首项ta10,1321nnnaaa,12n,,(1)若53t,求证11na是等比数列并求出{}na的通项公式;(2)若nnaa1对一切*Nn都成立,求t的取值范围。22.已知()2lnbfxaxxx在1x与12x处都取得极值。(I)求a,b的值;(Ⅱ)若对1[,1]4x时,()fxc恒成立,求实数c的取值范围。23.在数列{}na中,nS为其前n项和,满足2,(,*)nnSkannkRnN.(I)若1k,求数列{}na的通项公式;(II)若数列{21}nan为公比不为1的等比数列,且1k,求nS.24.已知数列{}na的首项ta10,1321nnnaaa,12n,,(1)若53t,求证11na是等比数列并求出{}na的通项公式;(2)若nnaa1对一切*Nn都成立,求t的取值范围。25.已知数列{}na的首项ta10,1321nnnaaa,12n,,(1)若53t,求证11na是等比数列并求出{}na的通项公式;(2)若nnaa1对一切*Nn都成立,求t的取值范围。26.已知数列na满足:11a;11nnaanN,。数列nb的前n项和为nS,且2,nnSbnN。⑴求数列na、nb的通项公式;⑵令数列nc满足annncb,求其前n项和为nT。27.已知f(x)=mx(m为常数,m>0且m≠1).设f(a1),f(a2),…,f(an)…(n∈N)是首项为m2,公比为m的等比数列.(1)求证:数列{an}是等差数列;(2)若bn=an·f(an),且数列{bn}的前n项和为Sn,当m=2时,求Sn;(3)若cn=f(an)lgf(an),问是否存在m,使得数列{cn}中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.28.已知数列{na}、{nb}满足:1121,1,41nnnnnbaabba.(1)求1,234,,bbbb;(2)求数列{nb}的通项公式;(3)设1223341...nnnSaaaaaaaa,求实数a为何值时4nnaSb恒成立29.已知等比数列na中641a,公比1q,且2a,3a,4a分别为某等差数列的第5项,第3项,第2项.⑴求数列na的通项公式;⑵设12lognnba,求数列nb的前n项和nT.30.已知数列{}na的首项*11,3121,53Nnaaaannn(1)求{}na的通项公式;(2)证明:对任意的*2),32()1(111,0Nnxxxaxnn.31.设函数210xfxxx,数列na满足1111,nnaafa*,2nNn且。⑴求数列na的通项公式;⑵设11223344511nnnnTaaaaaaaaaa,若2nTtn对*nN恒成立,求实数t的取值范围;⑶是否存在以1a为首项,公比为*05,qqqN的等比数列kna,*kN,使得数列kna中每一项都是数列na中不同的项,若存在,求出所有满足条件的数列kn的通项公式;若不存在,说明理由。32.设数列{an}中,a1=a,an+1+2an=2n+1(n∈N*).(Ⅰ)若a1,a2,a3成等差数列,求实数a的值;(Ⅱ)试问数列122nna能否为等比数列.若是等比数列,请写出相应数列{an}的通项公式;若不能,请说明理由解.(Ⅰ)123,24,4aaaaaa,33..等比数列}{na为递增数列,且,324a92053aa,数列2log3nnab(n∈N※)(1)求数列}{nb的前n项和nS;(2)122221nbbbbTn,求使0nT成立的最小值n.2012届高考数学(理)考前60天冲刺【六大解答题】数列专练1.数列}{na的前n项和记为nS,ta1,121()nnaSnN.(1)当t为何值时,数列}{na是等比数列;(2)在(I)的条件下,若等差数列}{nb的前n项和nT有最大值,且153T,又11ba,22ba,33ba成等比数列,求nT.解:(I)由121nnSa,可得121(2)nnaSn,两式相减得)2(3,211naaaaannnnn即,∴当2n时,}{na是等比数列,要使1n时,}{na是等比数列,则只需31212ttaa,从而1t.(II)设}{nb的公差为d,由153T得15321bbb,于是52b,故可设dbdb5,531,又9,3,1321aaa,由题意可得2)35()95)(15(dd,解得10,221dd,∵等差数列}{nb的前n项和nT有最大值,∴10,0dd∴2520)10(2)1(15nnnnnTn.2.已知数列na的首项114a的等比数列,其前n项和nS中3316S,(Ⅰ)求数列na的通项公式;(Ⅱ)设12log||nnba,12231111nnnTbbbbbb,求nT解:(Ⅰ)若1q,则333416S不符合题意,∴1q,……………………………2分当1q时,由131314(1)3116aaqSq得11412aq∴11111()()422nnna…………………………………………6分(Ⅱ)∵111221loglog()12nnnban……………………………………7分∴11111(1)(2)12nnbbnnnn………………………………………9分∴nT=12231111nnbbbbbb=111111()()()233412nn1122n(19)(本题满分14分)设数列{an}中,a1=a,an+1+2an=2n+1(n∈N*).(Ⅰ)若a1,a2,a3成等差数列,求实数a的值;(Ⅱ)试问数列122nna能否为等比数列.若是等比数列,请写出相应数列{an}的通项公式;若不能,请说明理由解.(Ⅰ)123,24,4aaaaaa,因为2132aaa,所以2(24)4aaa,得89a4分(Ⅱ)方法一:因为1*122()nnnaanN,所以11122nnnnaa,6分得:1111()2222nnnnaa,故若122nna是以1112222aa为首项,-1为公比的等比数列,则必须1a.故1a时,数列122nna为等比数列,此时1112[()(1)]222nnnaa,否则当1a时,数列122nna的首项为0,该数列不是等比数列.3.已知数列{}na的首项11a,且满足*1().41nnnaanNa(1)设1nnba,求证:数列{}nb是等差数列,并求数列{}na的通项公式;(2)设2nnncb,求数列{}nc的前n项和.nS解:(Ⅰ)141nnnaaa,1114nnaa,1114nnaa,14nnbb.数列nb是以1为首项,4为公差的等差数列.……………………………………3分114(1)nnbna,则数列na的通项公式为143nan.…………………6分(Ⅱ)12325292(43)2nnSn……………①2341225292(43)2nnSn………………②②①并化简得1(47)214nnSn.4.已知}{na是单调递增的等差数列,首项31a,前n项和为nS,数列}{nb是等比数列,首项.20,12,123221bSbab且(Ⅰ)求}{}{nnba和的通项公式。(Ⅱ)令}{),)(cos(nnnncNnaSC求的前n项和.nT解:(Ⅰ)设公差为d,公比为q,则22(3)12abdq322233(3)9320Sbabdqdq311,113dqqd2(3)(11)332312dddd,232210,(37)(3)0dddd,na是单调递增的等差数列,d>0.则3,2dq,3(1)33nann,12nnb………………6分(Ⅱ)2233,22cos33322nnnnSnnncSnSnnn是偶,是奇………………8分当n是偶数,123123412463(2)6121834nnnnnTccccSSSSSSnnaaaan………………10分当n是奇数,2213(1)(1)333(1)4224nnnnnTTSnnn………………12分综上可得23(2),43(1),4nnnnTnn是偶是奇5.已知数列{}na的前n项和为nS,若112,.nnnnnnaSanbaa且(1)求证:{1}na为等比数列;(2)求数列{}nb的前n项和。(1)解:由2nnSan得:1121nnSan∴111221nnnnnaSSaa,即121nnaa∴112(1)nnaa4分又因为1121Sa,所以a1=-1,a1-1=-2≠0,∴{1}na是以-2为首项,2为公比的等比数列.6分(2)解:由(1)知,11222nnna,即21nna8分∴11211(12)(12)2121nnnnnnb10分故223111111111[()()()]121212121212121nnnnT6.在数列na中,已知)(121,1*111Nnaaaaaannnnn且(I)求数列na的通项公式;(II)令132212111,)12(nnnnnccccccSac,若kSn恒成立,求k的取值范围。解析:(1)解:因为1211nnnnaaaa,所以21221nnnnaaaa,即22121221nnaa,………………………………………………2分令2,2112nnnnbbab,故nb是以41为首项,2为公差的等差数列。所以4781241nnbn,………………………………………………4分因为1na,故2781nan。…………………………………………6分(2)因为78122nacnn,所以181781811878111nnnnccnn,……………………8分所以181781171919118111113221nnccccccSnnn81181181n,………………………………10分因为kSn恒成立,故81k。8.已知数列na中,14a,12(1)nnaan,(1)求证:数列2nan为等比数列。(2)设数列na的前n项和为nS,若22nnSan,求正整数列n的最小值。解:因为12(1)2(2)nnanan所以12(1)22nnanan所以数列2nan为等比数列。(2)122a1222nnan22nnan1222nnsnn22nnSan可知5n时满足条件。9.已知数列{}na的前项和nS满足:(1)1nnaSaa(a为常数,且0a,1a).(Ⅰ)求{}na的通项公式;(Ⅱ)设21nnnSba,若数列{}nb为等比数列,求a的值.解:解:(Ⅰ)因为11(1)1aSaa,所以1aa当2n时,1111nnnnnaaaSSaaaa,1nnaaa,即以为a首项,a为公比的等比数列.∴1nnnaaaa;…………6分(Ⅱ)由(Ⅰ)知,2(1)(31)211(1)nnnnnaaaaaabaaa,若为等比数列,则有2213bbb,而13b,232aba,232322aaba故22232322()3aaaaa,解得13a再将13a代入得3nnb成等比数列,所以13a成立10.已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列.(1)求数列{an}的通项公式;(2)设Tn为数列{}的前n项和,若Tn≤λan+1对∀n∈N*恒成立,求实数λ的最小值.解:(1)设公差为d。由已知得121114614(2)(6)adadaad……………………3分解得1d或0d(舍去)所以12a,故1nan……………………………6分(2)因为11111(1)(2)12nnaannnn所以11111111233412222(2)nnTnnnnL……………………9分因为1nnTa对*nN恒成立。即,(2)2(2)nnn,对*nN恒成立。又211142(2)2(44)162(4)nnnn所以实数的最小值为11611.在各项均为正数的数列na中,已知点*1,()nnaanN在函数2yx的图像上,且24164aa.(Ⅰ)求证:数列na是等比数列,并求出其通项;(Ⅱ)若数列nb的前n项和为nS,且nnbna,求nS..【解】(Ⅰ)因为点*1(,)()nnaanN在函数12yx的图像上,所以12nnaa,…………………………1分且0na,所以112nnaa,故数列na是公比12q的等比数列.……………………3分因为24164aa,所以311164aqaq,即24111()264a,则112a,……………………………4分所以12nna…………………………………6分(Ⅱ)由(Ⅰ)知,12nna,所以1()2nnnbnan.…………………7分所以2111112(1)2222nnnSnn……①………………9分231111112(1)22222nnnSnn……②…………………10分①-②式得231111111222222nnnSn…………………11分即2111111112212122222212nnnnnnnSnn12.数列na中,已知)(121,1*111Nnaaaaaannnnn且(I)求数列na的通项公式;(II)令132212111,)12(nnnnnccccccSac,若kSn恒成立,求k的取值范围。解析:(1)解:因为1211nnnnaaaa,所以21221nnnnaaaa,即22121221nnaa,………………………………………………2分令2,2112nnnnbbab,故nb是以41为首项,2为公差的等差数列。所以4781241nnbn,………………………………………………4分因为1na,故2781nan。…………………………………………6分(2)因为78122nacnn,所以181781811878111nnnnccnn,……………………8分所以181781171919118111113221nnccccccSnnn81181181n,………………………………10分因为kSn恒成立,故81k。13.已知数列{}na的前n项和为nS,若112,.nnnnnnaSanbaa且(1)求证:{1}na为等比数列;(2)求数列{}nb的前n项和。(1)解:由2nnSan得:1121nnSan∴111221nnnnnaSSaa,即121nnaa∴112(1)nnaa4分又因为1121Sa,所以a1=-1,a1-1=-2≠0,∴{1}na是以-2为首项,2为公比的等比数列.6分(2)解:由(1)知,11222nnna,即21nna8分∴11211(12)(12)2121nnnnnnb10分故223111111111[()()()]121212121212121nnnnT.14.在数列{}na中,13a,122nnaan(2n≥且*)nN.(1)求2a,3a的值;(2)证明:数列{}nan是等比数列,并求{}na的通项公式;(3)求数列{}na的前n项和nS.(1)解:∵13a,122nnaan(2n≥且*)nN,∴212226aa,3223213aa.…………2分(2)证明:∵11111(22)2222(1)11nnnnnnanannanananan,∴数列{}nan是首项为114a,公比为2的等比数列.∴11422nnnan,即12nnan,∴{}na的通项公式为12nnan*()nN.…………8分(3)∵{}na的通项公式为12nnan*()nN,∴2341(2222)(123)nnSn2222(12)(1)821222nnnnnn*()nN.…………12分15.已知数列na满足222121naaann(Ⅰ)求数列na的通项;(Ⅱ)若nnanb求数列nb的前n项nS和。解:(Ⅰ)2111an时222213221naaaann(1)21222123221naaaann(2)(1)-(2)得2121nna即nna21(n2)又211a也适合上式nna21(Ⅱ)nnnb2nnnS22322213213222)1(22212nnnnnS(1)-(2)nS111222221)21(2nnnnnn111222221)21(2nnnnnn22)1(1nnnS16.已知正项数列}{na的前n项和为nS,且*,21NnSaannn.(Ⅰ)求证:数列}{2nS是等差数列;(Ⅱ)求解关于n的不等式84)(11nSSannn、;(Ⅲ)记数列32nnSb,nnbbbT11121,证明:nTnn123111.解:(Ⅰ)nnnSaa21.nnnSaa212.当2n时,nnnnnSSSSS)(21)(121,化简得1212nnSS.由11121aaa,得21211Sa.数列}{2nS是等差数列.…(Ⅱ)由(I)知nnSn)1(12,又由84)(11nSSannn,得84))((11nSSSSnnnn.84221nSSnn,即841n.49n.又*Nn,不等式的解集为}2,1{.(Ⅲ)当2n时,nnnnnnnnnnnnnnbn111)1(11)1(1211.nnnTn123)111)312)211(21(111)112(11)1(1211nnnnnnnnnnnnnbn.111)111.)31)211(nnnhTn,故nTnn12311117,已知递增的等比数列{}na满足234328,2aaaa且是24,aa的等差中项。(Ⅰ)求数列{}na的通项公式;(Ⅱ)若nnnSab,12log是数列{}nnab的前n项和,求.nS解:(1)设等比数列的公比为q,有题意可得4234324228aaaaaa解答:83aq=221q(舍去)nnnaa2233,∴等比数列na的通项公式为:nna2(2)∵1log12nabnn∴anbn=(n+1)2n,用错位相减法得:12nnns19.设na是公差不为零的等差数列,nS为其前n项和,满足222223457,7aaaaS,(1)求数列na的通项公式及前n项和nS;(2)试求所有的正整数m,使得12mmmaaa为数列na中的项。解:(1)设公差为d,则22222543aaaa,由性质得43433()()daadaa,因为0d,所以430aa,即1250ad,又由77S得176772ad,解得15a,2d,(2)12mmmaaa=(27)(25)23mmm,设23mt,则12mmmaaa=(4)(2)86ttttt,所以t为8的约数。20.已知等差数列na满足:37a,5726aa,na的前n项和为nS.(Ⅰ)求na及nS;(Ⅱ)令bn=211na(*nN),求数列nb的前n项和nT。解析:(Ⅰ)设等差数列na的公差为d,因为37a,5726aa,所以有112721026adad,解得13,2ad,所以321)=2n+1nan(;nS=n(n-1)3n+22=2n+2n。………………6分(Ⅱ)由(Ⅰ)知2n+1na,所以bn=211na=21=2n+1)1(114n(n+1)=111(-)4nn+1,所以nT=111111(1-+++-)4223nn+1=11(1-)=4n+1n4(n+1),即数列nb的前n项和nT=n4(n+1)。20.已知数列{an}的前n项和为Sn,且a1=1,nan+1=(n+2)Sn(n=1,2,3,…).(1)求证:数列{}为等比数列,并由此求出Sn;(2)若数列{bn}满足:b1=,=(n∈N*),试求数列{bn}的通项公式.解:(1)证明:由nan+1=(n+2)Sn,得n(Sn+1-Sn)=(n+2)Sn,即=2·,∴数列{}是首项为=a1=1,公比为2的等比数列,∴=2n-1,Sn=n2n-1.(2)由条件得==+2n-1.设cn=,则c1=,当n≥2时,cn=c1+(c2-c1)+(c3-c2)+…+(cn-cn-1)=2-1+20+21+…+2n-2=(2n-1),当n=1时,也满足上式.∴cn=(2n-1)(n∈N*),从而bn=ncn=(2n-1).21.已知数列{}na的首项ta10,1321nnnaaa,12n,,(1)若53t,求证11na是等比数列并求出{}na的通项公式;(2)若nnaa1对一切*Nn都成立,求t的取值范围。22.已知()2lnbfxaxxx在1x与12x处都取得极值。(I)求a,b的值;(Ⅱ)若对1[,1]4x时,()fxc恒成立,求实数c的取值范围。(1)由题意知,0na,nnnaaa31211,32311nnaa,1131111nnaa,11213a………………………………4分所以数列11na是首项为23,公比为13的等比数列;……………5分nnna3231135111,233nnna……………………8分(2)由(1)知1131111nnaa,1311111nnta……………10分由1130,21nnnaaaa知0na,故1nnaa得111nnaa……………11分即11111(1)()1(1)()133nntt得110t,又0t,则01t23.在数列{}na中,nS为其前n项和,满足2,(,*)nnSkannkRnN.(I)若1k,求数列{}na的通项公式;(II)若数列{21}nan为公比不为1的等比数列,且1k,求nS.解:(I)当1k时,2,nnSann所以21,(2)nSnnn即22(1)(1),(1)nSnnnnn,所以当1n时,112aS;当2n时,221(1)(1)2nnnaSSnnnnn所以数列{}na的通项公式为)(2Nnnan.…………7分(II)当2n时,112nnnnnaSSkakan,所以1(1)22nnkakan,111aSka.1k,10a,221ak,3246(1)kak212325378333,5,71(1)kkkaaakk由题意得,22130(5)(3)(7)aaa,所以32k.此时,1344nnaan,从而1213[2(1)1]nnanan因为121103,a所以210nan,从而{21}nan为公比为3的等比数列,得213nnan,231nnan,1233222nnSnn24.已知数列{}na的首项ta10,1321nnnaaa,12n,,(1)若53t,求证11na是等比数列并求出{}na的通项公式;(2)若nnaa1对一切*Nn都成立,求t的取值范围。(1)由题意知,0na,nnnaaa31211,32311nnaa,1131111nnaa,11213a………………………………4分所以数列11na是首项为23,公比为13的等比数列;……………5分nnna3231135111,233nnna……………………8分(2)由(1)知1131111nnaa,1311111nnta……………10分由1130,21nnnaaaa知0na,故1nnaa得111nnaa……………11分即11111(1)()1(1)()133nntt得110t,又0t,则01t18.(本题满分14分)等比数列}{na为递增数列,且,324a92053aa,数列2log3nnab(n∈N※)(1)求数列}{nb的前n项和nS;(2)122221nbbbbTn,求使0nT成立的最小值n.解:(1)}{na是等比数列,92032412131qaqaqa,两式相除得:10312qq313qq或者,}{na为增数列,3q,8121a-------4分5111323812nnnnqaa--------6分52log3nabnn,数列}{nb的前n项和)9(212)54(2nnnnSn---8分(2)122221nbbbbTn=)52()52()52()51(12n=052121nn即:152nn-------12分1452,1452545minn--------14分(只要给出正确结果,不要求严格证明)25.已知数列{}na的首项ta10,1321nnnaaa,12n,,(1)若53t,求证11na是等比数列并求出{}na的通项公式;(2)若nnaa1对一切*Nn都成立,求t的取值范围。(1)由题意知,0na,nnnaaa31211,32311nnaa,1131111nnaa,11213a………………………………4分所以数列11na是首项为23,公比为13的等比数列;……………5分nnna3231135111,233nnna……………………8分(2)由(1)知1131111nnaa,1311111nnta……………10分由1130,21nnnaaaa知0na,故1nnaa得111nnaa……………11分即11111(1)()1(1)()133nntt得110t,又0t,则01t12在数列na中,ccaaann(,111为常数,)Nn,且521,,aaa成公比不等于1的等比数列.(Ⅰ)求c的值;(Ⅱ)设11nnnaab,求数列nb的前n项和nS解:(Ⅰ)∵cacaann,1,1为常数,∴cnan)1(1.………………2分∴caca41,152.又521,,aaa成等比数列,∴cc41)1(2,解得0c或2c.…4分当0c时,nnaa1不合题意,舍去.∴2c.…………………6分(Ⅱ)由(Ⅰ)知,12nan.………………………………………………8分∴)121121(21)12)(12(111nnnnaabnnn…………10分∴)121121()5131()311(2121nnbbbSnn12)1211(21nnn…………………………………………12分26.已知数列na满足:11a;11nnaanN,。数列nb的前n项和为nS,且2,nnSbnN。⑴求数列na、nb的通项公式;⑵令数列nc满足annncb,求其前n项和为nT。解:(1)由已知得数列na为等差数列,首项为1,公差为1.所以其通项公式为nan····················3分因为1122nnnnSbSb,所以112nnbb,所以数列nb为等比数列,又11121Sbb所以112nnb(2)由已知得:12112312222nnnnncnT,所以23111231222222nnnnnT所以231111111112121122222222212nnnnnnnnnnT所以1112414222nnnnnnT27.已知f(x)=mx(m为常数,m>0且m≠1).设f(a1),f(a2),…,f(an)…(n∈N)是首项为m2,公比为m的等比数列.(1)求证:数列{an}是等差数列;(2)若bn=an·f(an),且数列{bn}的前n项和为Sn,当m=2时,求Sn;(3)若cn=f(an)lgf(an),问是否存在m,使得数列{cn}中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.解:(1)由题意f(an)=m2·mn+1,即man,=mn+1.∴an=n+1,(2分)∴an+1-an=1,∴数列{an}是以2为首项,1为公差的等差数列.(4分)(2)由题意bn=anf(an)=(n+1)·mn+1,当m=2时,bn=(n+1)·2n+1∴Sn=2·22+3·23+4·24+…+(n+1)·2n+1 ①(6分)①式两端同乘以2,得2Sn=2·23+3·24+4·25+…+n·2n+1+(n+1)·2n+2 ②②-①并整理,得Sn=-2·22-23-24-25-…-2n+1+(n+1)·2n+2=-22-(22+23+24+…+2n+1)+(n+1)·2n+2=-22-+(n+1)·2n+2=-22+22(1-2n)+(n+1)·2n+2=2n+2·n.(9分)(3)由题意cn=f(an)·lgf(an)=mn+1·lgmn+1=(n+1)·mn+1·lgm,要使cn1时,lgm>0,所以n+1m对一切n∈N*成立,因为=1-的最小值为,所以01时,数列{cn}中每一项恒小于它后面的项.(13分)28.已知数列{na}、{nb}满足:1121,1,41nnnnnbaabba.(1)求1,234,,bbbb;(2)求数列{nb}的通项公式;(3)设1223341...nnnSaaaaaaaa,求实数a为何值时4nnaSb恒成立解:(1)11(1)(1)(2)2nnnnnnnnbbbaabbb+∵1113,44ab∴234456,,567bbb……………4分(2)∵11112nnbb∴12111111nnnnbbbb∴数列{11nb}是以-4为首项,-1为公差的等差数列……………6分∴14(1)31nnnb∴12133nnbnn……………8分(3)113nnabn∴12231111114556(3)(4)444(4)nnnnSaaaaaannnn∴22(1)(36)8443(3)(4)nnannananaSbnnnn……………10分由条件可知2(1)(36)80anan恒成立即可满足条件设2()(1)3(2)8fnanana=1时,()380fnn恒成立,a>1时,由二次函数的性质知不可能成立a










 东城区2011高三一模(文科)数学试卷+参考答案
东城区2011高三一模(文科)数学试卷+参考答案 2016年天津高考文科数学试卷+参考答案解析(Word版)
2016年天津高考文科数学试卷+参考答案解析(Word版)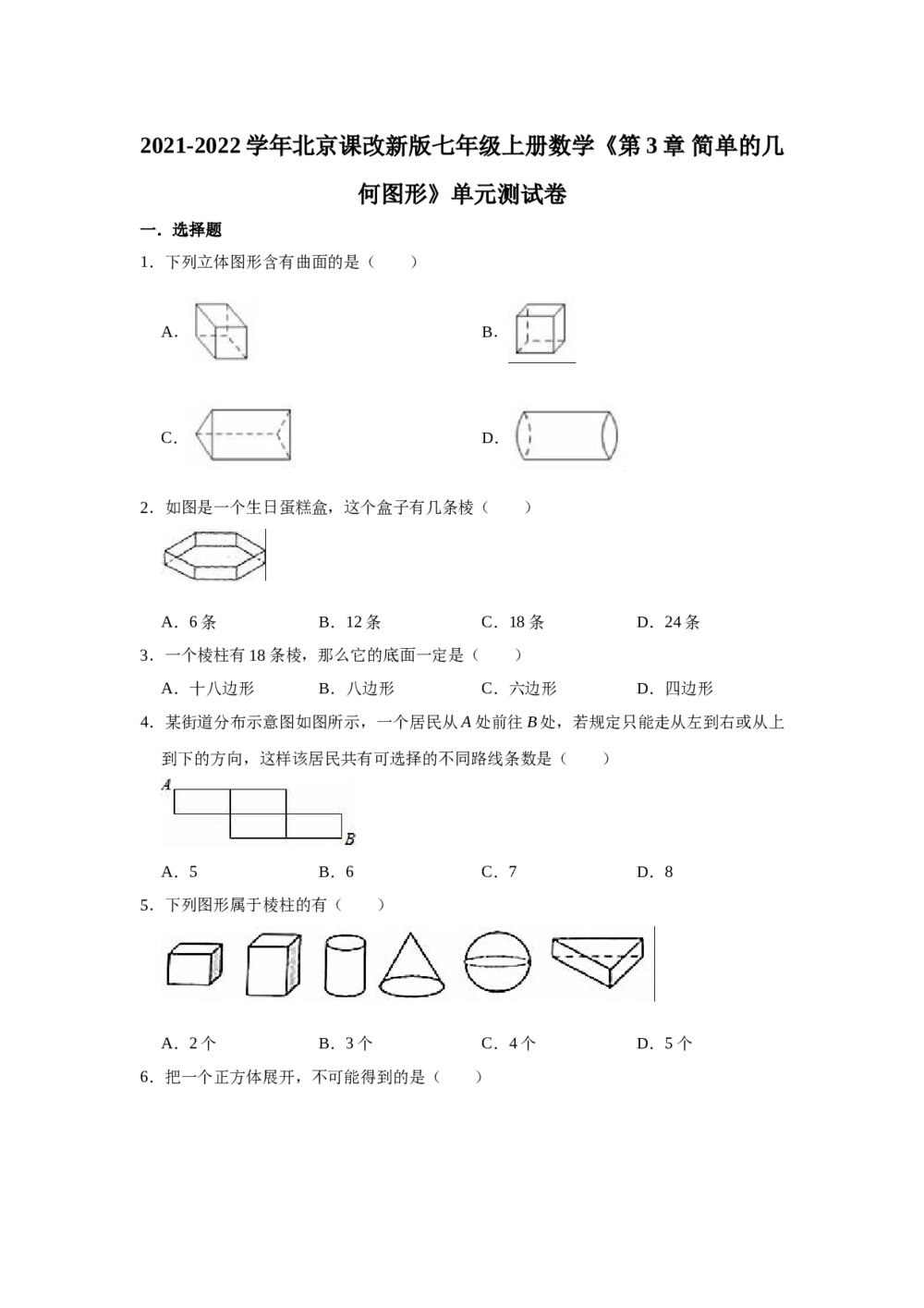 2021-2022学年北京课改新版七年级数学上册《第3章 简单的几何图形》单元测试卷word版+参考答案
2021-2022学年北京课改新版七年级数学上册《第3章 简单的几何图形》单元测试卷word版+参考答案 六年级下册数学期末考试试卷+参考答案
六年级下册数学期末考试试卷+参考答案 2012高考数学备考冲刺之易错点点睛系列专题 概率与统计(理科)(教师版)
2012高考数学备考冲刺之易错点点睛系列专题 概率与统计(理科)(教师版) 2021年全国高考甲卷数学(文科)试题试卷+(答案解析)
2021年全国高考甲卷数学(文科)试题试卷+(答案解析)